Summary
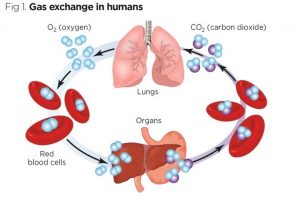
The binding and buffering of O2 and CO2 in the blood influence their exchange in the lungs and tissues and their transport through the circulation. To investigate binding and buffering effects, a model of gas exchange between blood and tissue is used. The model of exchanging Oxygen and Carbon Dioxide explains haemoglobin saturation, the simultaneous binding of o2 CO2. H+, 2,3-DPG to haemoglobin and temperature effects. Invertible Hill-type saturation equations facilitate rapid calculation of the redistribution of respiratory gases between plasma, red blood cells, and emission that occurs along concentration gradients in the lung and gas exchange regions. hair tissue.
These equations are suitable for the analysis of transients in tissue metabolism and partial pressures of the inhaled gas. The model illustrates that because red blood cell velocities in flowing blood are higher than plasma velocities after a transient, there can be long-lasting differences between plasma and red blood cell oxygen partial pressures. The blood-tissue gas exchange model has been incorporated into a higher-level model of the circulatory system, in addition to lung mechanics and gas exchange using the RBC and plasma equations to account for pH and CO2 buffering in the blood.
Model Description
- Region of pulmonary blood exchange
The lung module is composed of three compartments in series: a low compliance compartment representing the oral/nasal cavity and cartilaginous airways, a moderately compliant compartment characterizing collapsible bronchial airways, and a high compliance compartment. which resembles the alveolar space. In the model, the lung can be ventilated by positive pressure or by periodic chest expansion that reduces intrapleural pressure, resulting in bidirectional airflow and inflation and deflation of the lung.
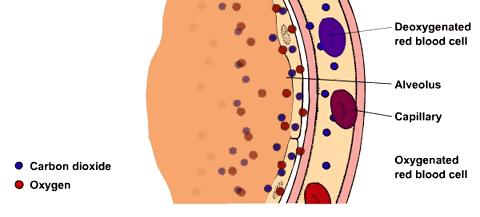
The convective flow between compartments is modelled as pressure-driven flow through a resistor. The equations for the convective and diffusive transport of oxygen and carbon dioxide between adjacent lung compartments are similar to those used in previous models. Each lung compartment is assumed to be well mixed. The alveolar compartment exchanges respiratory gases with the plasma region of a blood tissue exchange unit, which contains a region of red blood cells surrounded by a region of the plasma. The inhaled partial pressure of each species is an input to the model.
- Arterial and venous convective regions
Blood from the pulmonary capillaries is transported through non-exchangeable convective channels (left atrium, left ventricle, aorta, arteries) to the tissue. The solute exchange between red blood cells and plasma continues. Plasma red blood cell concentration differences persist when their velocities differ. Metabolism is zero, but buffer reactions continue. Values for the ratio of RBC to plasma velocity in arteries and veins were taken to be 1.1 and 1.05, respectively, although the choice of these numbers depends on the range of diameters represented.
- Numerical methods and simulation procedures
Numerical methods are those previously described using a Lagrangian sliding fluid element algorithm. Other partial differential equation solvers (Mac-Cormack, TOMS 731) are also available under the JSim simulation system. The values of the parameters in this model were those used previously with some exceptions. The flow rate is allowed to range between 5 L/min at rest and 25 L/min during exercise.
In addition, the product of the permeability surface area of red blood cells (PSRBC) has been recalculated according to experimental evidence to reflect the combination of a small obstacle to its membrane permeation and the times required for the permeation of red blood cells. union and disunion. The haemoglobin equations incorrectly assume instantaneous equilibrium instead of taking several milliseconds. The lung model described here is similar in structure to the model of Lutchen et al.
Results and Discussion
Two cases are examined in this study. The former refers to the transport of respiratory gases during normal and elevated ventilation, perfusion, and metabolism. For normal levels, parameters are the respiratory rate of 12 breaths/min, tidal volume of ~500 mL driven by 10 mmHg inspiratory positive pressure at the mouth for 2 seconds, and inspired air with PO2 = 150 and PCO2 = 0 mmHg. Blood flow was set at ~5 L/min, and metabolic rate was adjusted so that pulmonary terminal capillary blood O2 and CO2 partial pressures were ~100 and ~40 mmHg, while venous values were 70. and 45mmHg. The final tidal PO2 was 105 and the PCO2 was 34 mmHg.
The second case focuses on the balance of O2 between plasma and red blood cells as it enters the arterial region and the effect of the relative velocity difference between plasma and red blood cells on the balance. To investigate equilibrium, the plasma oxygen partial pressure is increased from 25 to 100 mmHg and transient effects are observed. To investigate the effect of the relative velocity difference, a pulsed increase in plasma PO2 is applied at the upstream end and the difference between plasma and red blood cell PO2 is quantified along the arterial region.
Conclusions
We have linked a series of blood-tissue gas exchange models with a lung gas transport model to describe the respiratory gas exchange between the lung and tissue via circulating blood. We illustrate that changes in metabolism that cause increases in CO2 production and O2 consumption can be offset by simultaneous increases in ventilation and perfusion. O2 gradients between plasma and red blood cells can persist along the pulmonary capillary and in the arterial system because red blood cells have higher velocities than plasma. The model is ideal for investigating questions related to the integrative effects of pulmonary ventilation, chemical binding kinetics, vascular transport, and tissue metabolism on whole-body respiratory gas exchange.